我无语了,我准备了一个月的编程题和离散题,最后却问了我算法和命题的概念
2020年的博士前期情报系统秋入试,平心来说绝对是最近很多年来名大情系考的最简单的一次了;怎么个简单法,考试前提前告知:删去了以前的概率统计部分(等于名大不考跟高数有关的任何数学),并且增加了计算机网络、操作系统、算法,考的都是概念,基本不含任何计算,但是时间紧迫,基本没有时间想,看到题目不能张口就说那基本这题就没了。
口头面试的流程大概是下午一点报道(JST),然后和几个同面试场的考生在等待室里闭麦等着,大概一点四十五分监考会说你可以断开链接,去连接考场的会议室了,从等待室里退出来以后就直接输入之前抄的考场会议室号码,连上之后等到两点开考才会放你进去。
考试两点钟正式开始,是我报的第一志愿监的考,上来先简单和你介绍一下怎么答题:一会会给你看11题,你要从当中挑三道,但是挑完之后就不可以更换,挑完之后我们会一道题一道题问你,你答完的题目不可以再回去修改,问题主要通过口头表述,放在PPT的大概就是个问题的方向,你可以用纸来解释,一题大概之后五分钟的时间,之后还有7分钟是问一般问题。
離散数学、オートマトン形式言語、アルゴリズム、論理学、コンパイラ、プログラミング、論理設計、計算機アーキテクチャー、オプレーティングシステム、情報ネットワーク、ソフトウェア設計法
明白了之后就是放题目,11题在屏幕上摞了两列,左边一列主要是离散数学的概念,还有软件开发的概念?,以及计组的概念题,都是很短的题目,几个字;右边放了一段代码:
int combine(int n, int m){
if (m==0 || n==m){
return 1;
}
else{
return combine(n-1, m) + combine(n-1, m-1);
}
}
这段代码计算的是组合数,我当时并不知道,知识因为之前做过去问,编程题往往都能做出来,所以准备代码题无脑选上,然后再选离散和操作系统。用了大概几十秒把11题扫了一遍,排掉我看不懂的片甲单词,排掉看得懂但是不知道是啥的汉字,最后选了【命题公式的可充分性证明】,【PAGE FAULT】和【combine,上面那段代码】
考官让我挑一题入手,以往经验代码题最简单,我便说了11题。之后考官就直接问了,“这段代码的作用是什么”。我才刚刚开始读代码,把代码扫了一遍,似乎是递归从n加到m,又从n加到m-1,这到底计算了什么?正在想的时候,面试官说想不出来可以先问你下一小问,这个问题一会还可以回答。哦,那只能先下一小问了,没时间了。下一小问很简单,“这个函数使用的自己调用自己的方法叫什么?”迭代调用啊,迭代的日文是什么????迭代的英文是什么????好像是it…iter….iterarative?我含糊不清的说出这个单词,面试官说没听清,我慌忙写下“迭代”两字,考官看不懂笑了,这尼玛写的中文吧(迭代日文是イテレータ),最后只能莽的说了一个iterative重音还发在了it上,十分滑稽。(其实根本就不是迭代,是递归,recursive,再帰。) “那行吧,你能不能告诉我他的复杂度是什么?用n来表示。” 其实我根本没听懂他问的是什么,那个关键的词没听懂,但是隐约感觉是要问复杂度了。这个算法的复杂度,递归调用自己那是不是n的平方,所以我瞎几把写了O(n^2) (其实之前还在纸上算了一会这函数的内容,造成这个时候已经没有时间再在这道题停留了,其他监考老师在催下一题。),放到镜头前给他看,“n二乗ですね。”之后他又问了我一下有没有想出来这个函数是做什么用的,我写了一个 给他看。
给他看。
其实这都是错的,复杂度是 ,计算的结果是
,计算的结果是 ,最后的那个return是组合数公式:
,最后的那个return是组合数公式:


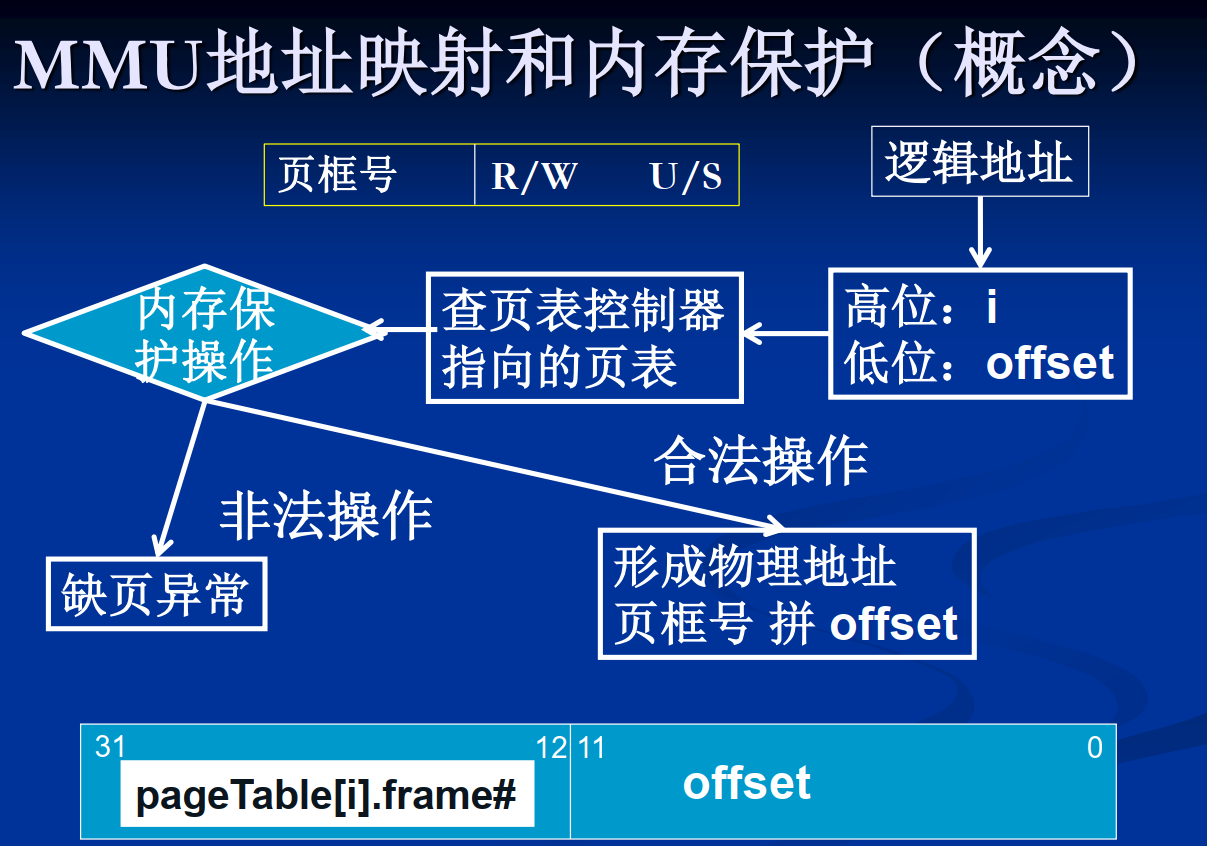
第一题做完之后,花了很多时间,根本没做出来,考官让我快点,剩下两题里先挑一个有自信的。我果断选了内存缺页,“介绍一下内存缺页是什么吧”,我本来就比较熟悉操作系统,上午刚好复习了内存缺页,就用英文解释了一下,程序要访问逻辑地址的时候,逻辑地址的内存不在实际的物理内存中,CPU报一个缺页中断(interrupt我说了error),然后去硬盘或者SWAP里把虚拟内存搬到实际的物理内存里,之后提供程序正常访问内存。之后又问了一下,你能不能讲一下逻辑地址是怎么转换成物理地址的?这个上午刚刚看过课件,我说是用逻辑地址去页表里查物理地址,然后简单画了个逻辑页面->页表->物理页面的图,之后又问我能不能再讲的详细一点?我说我不知道了,然后就下一题了。

最后一题,完全就是踩坑了,这个命题的可充分性,应该不是我想的那个成真赋值就可以的可充分,他问我你说说怎么证明可充分性,我说有两种方法,一是列真值表(Truth Table),另一个是通过公式,将原方程变换成另一个可以证明成立的方程;他问怎么变换呢,变换成什么形式呢?我想说变成最小合取范式,根本不记得这玩意英文怎么讲,就记得什么DFD CFN之类的缩写,(合取范式 Conjunctive normal form 連言標準形れんげんひょうじゅんけい 析取范式 Disjunctive normal form 選言標準形 せんげんひょうじゅんけい)最后支支吾吾啥也没说出来,他说那好吧那你说的另一种方法是什么?我说列真值表,true table,列出所有可能的情况,看看有没有一种情况下公式成立。
离散数学以前卷子都是算术题,我以为他会给我个公式让我去写一写证明公式可充分,结果一点公式都没有,全是嘴上讲的,这谁知道怎么讲啊,都是看的中文资料,偶尔看过几个CNF DNF之类的那种紧张的情况下也想不起来,youtube上的离散数学还都是印度咖喱英语,听都不想听/
三题全问完之后就是问一些入学的,你为什么想来,你愿不愿意接受调剂,你是不是报了别的学校,你毕业是升学还是入职
之后让你抄下考完试等待室的号码,之后断开会议,加入等待室会议。
等待室里就是日本老哥互相瞪眼,百般聊赖,比较尴尬的是日本人都穿了西服领带,至少至少也是件白衬衫,我就穿了个T恤,真的太尬了,T恤领子还很大,比较旧的T恤(。
总结来说,这次一是算法不精,那个算法呢,那个时间下,以前没看过的肯定是没法推导出来的,不过如果数学熟悉,可能能一眼看出来那是个组合数递推公式?但是我早忘了组合,以为不考数学就也没复习,没想到这种形式上还是考到了。如果能看出来是递推公式,每次+1应该很容易想出来复杂度等于组合数。内存缺页答得还行,从逻辑地址转物理地址的详细过程不知道,今天可以去搞清楚。离散数学命题那题完全就是踩坑了,wdnmd,谁知道会一点公式都没有,全都是讲的,然后全都不会讲,下次复习一定一定要见到所有中文词和符号吗,都背出来对应的日文和英文,我寻思你要去日本上课的,符号都不会说,那还学个几把。
3 thoughts to “名古屋大学情报系统秋入试体验”
感谢先辈 分享 请问您是上了么, system的人多么?我打算今年去逝世
非常感谢您的回答 祝您生活愉快
没上(捂脸) 当了半年远程研究生,同时在国内互联网公司实习,公司给的offer很香就直接留下了工作了,冬入也没报名(捂脸
谢谢您的回答,祝您生活愉快,我也要去卷了