Neo4j 自带算法库 学习笔记

Graph Algorithms 库

算法1 The Common Neighbors algorithm

通用邻居算法

计算公式：
其中N(x)是与节点相邻的节点集x，N(y)是与节点相邻的节点集y。

公式相当于计算从节点x与节点y的相邻节点的交集，等于从x出发经过两跳到达y的路径数

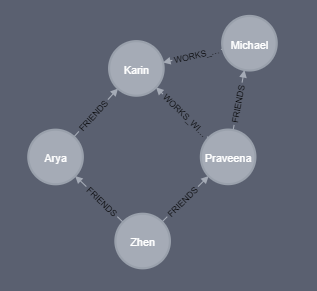
创建一个示例图：
MERGE (zhen:Person {name: "Zhen"})
MERGE (praveena:Person {name: "Praveena"})
MERGE (michael:Person {name: "Michael"})
MERGE (arya:Person {name: "Arya"})
MERGE (karin:Person {name: "Karin"})

MERGE (zhen)-[:FRIENDS]-(arya)
MERGE (zhen)-[:FRIENDS]-(praveena)
MERGE (praveena)-[:WORKS_WITH]-(karin)
MERGE (praveena)-[:FRIENDS]-(michael)
MERGE (michael)-[:WORKS_WITH]-(karin)
MERGE (arya)-[:FRIENDS]-(karin)

返回Michael和Karin的共同邻居数：
MATCH (p1:Person {name: 'Michael'})
MATCH (p2:Person {name: 'Karin'})
RETURN algo.linkprediction.commonNeighbors(p1, p2) AS score

执行
MATCH (p1:Person {name: 'Zhen'})
MATCH (p2:Person {name: 'Karin'})
RETURN algo.linkprediction.commonNeighbors(p1, p2) AS score

输出
2.0

执行
MATCH (p1:Person {name: 'Michael'})
MATCH (p2:Person {name: 'Karin'})
RETURN algo.linkprediction.commonNeighbors(p1, p2) AS score

输出
1.0

算法2 Weakly Connected Components algorithm

弱连接组件算法

WCC算法在无向图中找到一组连接的节点，其中同一组中的所有节点形成一个连接的组件。通常在分析的早期使用WCC来了解图形的结构。

算法3 Louvain算法

Louvain社区检测方法是一种用于检测网络中社区的算法。它最大化了每个社区的模块化评分，其中模块化量化了节点向社区的分配质量。这意味着，与社区在随机网络中的连接程度相比，评估社区中节点的连接密度更高。

CALL algo.beta.louvain(label: STRING, relationship: STRING, {
 write: BOOLEAN,
 writeProperty: STRING
 // additional configuration
})
YIELD nodes, communities, modularity, loadMillis, computeMillis, writeMillis

Louvian算法就是基于模块度Q的社区划分算法，简单的说，就是一组构成社区的节点，节点之间连接（社区内）越多，节点与外部连接（社区外）连接越少，模块度Q就越高。

通过Louvain获取一个社区里的全部节点和边：
call algo.louvain.stream() yield nodeId, community match (n) where id(n)=nodeId and community=1 with collect(n) as ns match (p)-[r]-(q) where q in ns and p in ns and q <> p return q,p,r;

直接调用Louvain
call algo.louvain.stream()