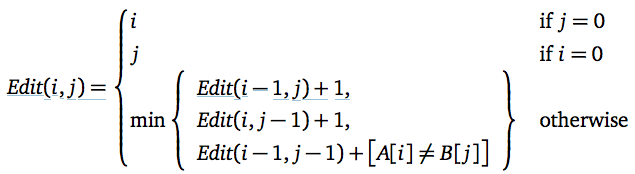编辑距离是衡量两个字符串S和T相似程度的一种度量方法。
编辑距离定义:将字符串S通过插入、删除、替换三种编辑操作,转变为字符串T,所需最少的编辑次数。
计算编辑距离的问题,符合动态规划的几个特征:
- 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。最优子结构性质为动态规划算法解决问题提供了重要线索。
- 无后效性。即子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响。
- 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率。
因此考虑用动态规划求解。
设字符串S,T长度分别为m, n,记S(i)为S从第1个字符到第i个字符之间的子串。S(0)表示空串,S(m)表示S本身。
因此,S和T间的编辑距离,可由S(i)和T(j)的编辑距离计算而来。
递推公式为:
具体的算法参见维基百科。
这个算法的特点是,S和T字符串左边始终是对齐的。为了更好地理解这个算法中的递推公式,我们把两个字符串按照特定方式对齐。
以字符串S=ALGORITHM和T=ALTRUISTIC为例:
S和T的字符对齐方式为,假设我们已经知道最优的编辑方式:
- 如果删去S中字符,则该字符对齐T中的空格
- 如果删去T中字符,则该字符对齐S中的空格
- 如果替换S中字符为T中字符,则这两个字符对齐
这种对齐方式有助于我们理解上述递推公式。
首先,我们不需要理会S和T左端是否对齐。
其次,注意到S(i)和T(j)的右端,只有三种可能性:
- S(i)右端在T(j)右端的右侧
- S(i)右端正对着T(j)右端
- S(i)右端在T(j)右端的左侧
这也是上述递推公式三种可能性的由来。
参考:Section5.5 — http://jeffe.cs.illinois.edu/teaching/algorithms/notes/05-dynprog.pdf